Controlling Propagation of Epidemics via Mean-Field Games

PDF

This page briefly describes the paper, Controlling Propagation of Epidemics via Mean-Field Games [1]. To see the details, check the PDF link above.

In this project, we proposed a new mean-field optimal control formulation to control the propagation of epidemics. Consider one of the simplest epidemiologic models, Susceptible-Infective-Recovered (SIR) model

\begin{equation*}\begin{aligned} \frac{dS(t)}{dt} &= -\beta S(t) I(t)\\ \frac{dI(t)}{dt} &= \beta S(t) I(t) - \gamma I(t)\\ \frac{dR(t)}{dt} &= \gamma I(t) \end{aligned}\end{equation*}

where \(S,I,R\) represent the numbers of susceptible, infected, and recovered populations, respectively. Susceptible people become infected with an infection rate \(\beta\) and infcetious people become recovered with a recovery rate \(\gamma\). Note that the model computes the dynamics of the total number of populations of each group, \( \{S,I,R\} \), without giving local spatial information. We extend this system of ODEs to the following system of PDEs.

\begin{equation}\label{eq:spatial-SIR}\begin{aligned} & \partial_t \rho_S + \nabla \cdot (\rho_S v_S) + \beta \rho_S \rho_I - \frac{\eta_S^2}{2}\Delta \rho_S = 0\\ & \partial_t \rho_I + \nabla \cdot (\rho_I v_I) - \beta \rho_S \rho_I + \gamma \rho_I - \frac{\eta_I^2}{2}\Delta \rho_I = 0\\ & \partial_t \rho_R + \nabla \cdot (\rho_R v_R) - \gamma \rho_I - \frac{\eta_R^2}{2}\Delta \rho_R = 0 \end{aligned}\end{equation}

where \(\rho_i:[0,T]\times\Omega\rightarrow [0,\infty) \,(i\in S,I,R)\) are the population densities of each group and \(v_i:[0,T]\times\Omega\rightarrow \mathbb{R}^d \,(i\in S,I,R)\) are velocity fields of each group on a spatial domain \(\Omega\subset \mathbb{R}^d\). Using this spatial SIR model, we introduce the mean field optimal control formulation,

\begin{equation}\label{eq:min-SIR} \begin{aligned} &\inf_{\rho_i,v_i} E(\rho_I(T,\cdot)) + \int^T_0 \sum_{i=S,I,R} \int_\Omega \frac{\alpha_i}{2} \rho_i |v_i|^2\, dx + F((\rho_S+\rho_I+\rho_R)(t,\cdot))\, dt\\ &\text{subject to \eqref{eq:spatial-SIR}, given } \rho_i(0,\cdot)\,(i=S,I,R) \end{aligned} \end{equation}

where \(E,F\) are lower semi-continuous and convex functionals, for example

\begin{equation*} E(u) = \int_\Omega u^2(x) \,dx,\quad F(u) = \int_\Omega u^2(x) \,dx. \end{equation*}

The functional \(E(\rho_I(T,\cdot))\) is the terminal cost that minimizes the total mass of infectious population density at the terminal time \(T\). The function \(\frac{\alpha_i}{2}\rho_i|v_i|^2\) is the transportation cost of the population density of each group \(i=S,I,R\). The functional \(F((\rho_S+\rho_I+\rho_R)(t,\cdot))\) represents the concentration of population at each time \(t\in[0,T]\). In sum, the minimization problem \eqref{eq:min-SIR} finds optimal velocities and densities such that evolutions of densities minimize the total number of infectious people at the terminal time while minimizing transportation costs and the concentration of population.

Note that this is a nonconvex optimization problem with a nonlinear constraint. We developed an algorithm based on general proximal primal-dual hybrid gradient (G-prox PDHG) method [2]. Below, we present some of the results generated by the algorithm. We set \(\beta=0.6,\gamma=0.1\). The videos show the evolution of densities from the solutions of the minimization problem (labeled with control) and the solutions of the following system of PDEs without velocity fields control (labeled without control):

\begin{equation*}\begin{aligned} & \partial_t \rho_S(t,x) + \beta \rho_S(t,x) \rho_I(t,x) = 0\\ & \partial_t \rho_I(t,x) - \beta \rho_S (t,x)\rho_I(t,x) + \gamma \rho_I(t,x) = 0\\ & \partial_t \rho_R(t,x) - \gamma \rho_I(t,x) = 0. \end{aligned}\end{equation*}

Example

Without control

With control

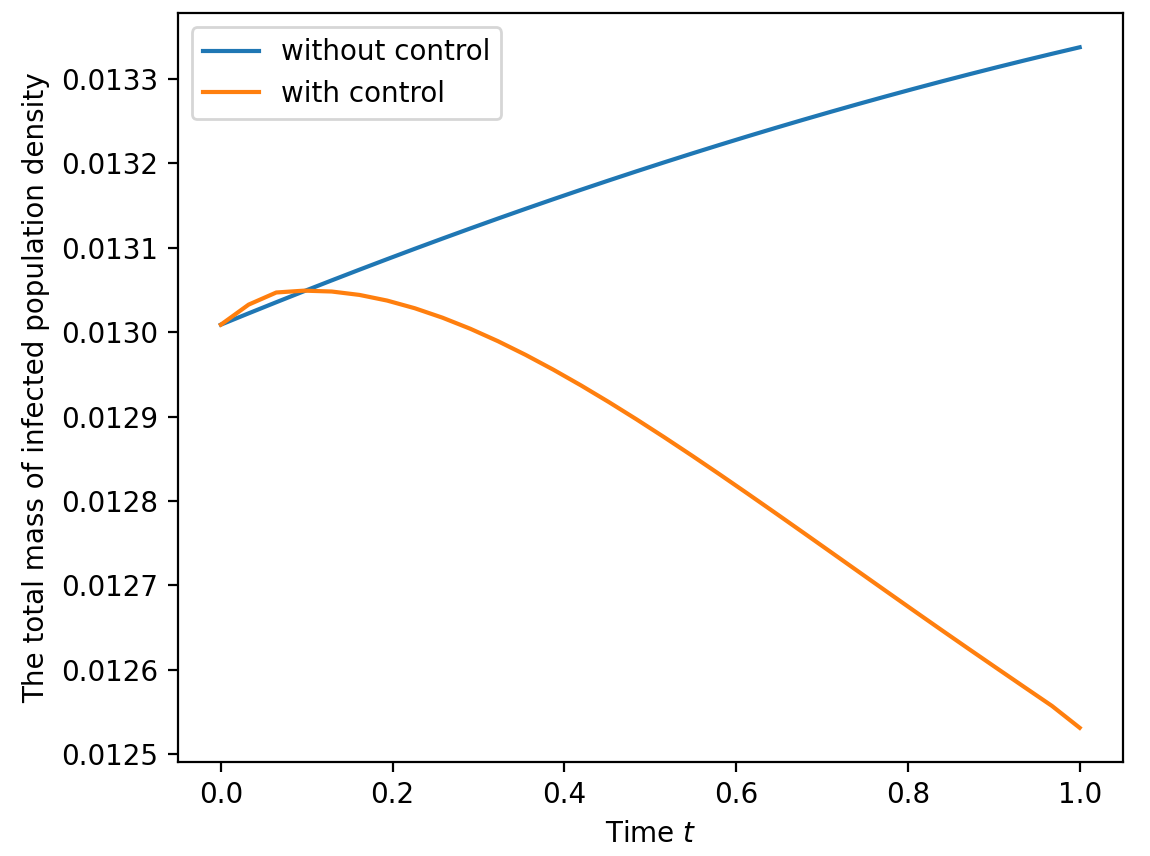
The solution from the minimization problem \eqref{eq:min-SIR} moves the susceptible population density away from the region where infectious population density is located. As a result, the solution finds a better strategy to reduce the total mass of infected population denstiy at the terminal time (0.0125 with control vs. 0.0133 without control).

Comparison of the total number of infected people between with and without control

References

[1] Wonjun Lee, Siting Liu, Hamidou Tembine, Wuchen Li, and Stanely Osher. Controlling propagation of epidemics via mean-field games. 2020.

[2] Matt Jacobs, Flavien Leger, Wuchen Li, and Stanley Osher. Solving Large-Scale Optimization Problems with a Convergence Rate Independent of Grid Size. SIAM Journal on Numerical Analysis., 57(3), 1100-1123, 2019.

Home